 |
David Jensen, Michael Atighetchi, Régis Vincent, Victor Lesser
Computer Science Department
University of Massachusetts at Amherst
Amherst, MA 01003
{jensen,adi,vincent,lesser}@cs.umass.edu
Copyright ©1999, American Association for Artificial Intelligence (www.aaai.org). All rights reserved.
Multiagent coordination frameworks often assume that agents possess accurate knowledge of the relationships among actions and the basic performance characteristics of those actions (e.g., cost and duration). Such knowledge allows agents to schedule activities in ways that exploit beneficial relationships, and avoid pathological ones. Unfortunately, accurate knowledge of NLEs is difficult to maintain in heterogeneous and open systems. Agent designers may not know the future operating environment for their agents, the complete set of actions open to other agents, and the effects those actions have on their own agents. For all of these reasons, the ability for multiagent systems to autonomously learn coordination knowledge appears critical for next-generation coordination frameworks [Sugawara and Lesser1998].
We investigated and implemented techniques to learn the statistical knowledge about NLEs represented in one well-established framework for multiagent coordination (TÆMS). We found that a combination of three simple learning techniques can be surprisingly effective. The learned knowledge can be used to accurately predict the performance of a particular action, given its context within a set of actions executed by the same agent or other agents. The success of these methods demonstrates how coordination knowledge can be learned explicitly, as opposed to learning coordination policies that implicitly represent knowledge of agents, environments, and their association.
In contrast, we explore learning explicit quantitative knowledge needed by deliberative agents -- agents that explicitly plan sequences of actions and that can trace the assumptions embedded in those plans. We assume that the coordination framework (TÆMS in this case) encodes all relevant characteristics of the environment needed to guide coordination and that agents can use this knowledge to devise coordinated actions. Separating knowledge from coordination mechanisms provides opportunities (e.g., the coordination strategy can be changed without altering the knowledge), as well as costs (e.g., using the knowledge requires explicit reasoning).
Another theme of learning for multiagent coordination has been learning to predict the future actions of other agents. Such predictions can help produce coordinated actions even without explicit communication among agents. Hu and Wellman [Hu and Wellman1998] study this type of learning in the context of a simulated double auction. Similarly, Zeng and Sycara [Zeng and Sycara1997] study learning to pre
Learning for multiagent coordination has become a popular topic in the past several years. Much of the existing work aims to equip agents with effective policies -- functions that map environmental conditions directly to coordinated actions. For example, Weiß [Weiß1998] investigates reinforcement learning (RL) techniques to improve the coordinated performance of reactive agents. Similarly, Tan [Tan1998] investigates how to extend RL to create coordinated multiagent policies.
In contrast, we explore learning explicit quantitative knowledge needed by deliberative agents -- agents that explicitly plan sequences of actions and that can trace the assumptions embedded in those plans. We assume that the coordination framework (TÆMS in this case) encodes all relevant characteristics of the environment needed to guide coordination and that agents can use this knowledge to devise coordinated actions. Separating knowledge from coordination mechanisms provides opportunities (e.g., the coordination strategy can be changed without altering the knowledge), as well as costs (e.g., using the knowledge requires explicit reasoning).
Another theme of learning for multiagent coordination has been learning to predict the future actions of other agents. Such predictions can help produce coordinated actions even without explicit communication among agents. Hu and Wellman [Hu and Wellman1998] study this type of learning in the context of a simulated double auction. Similarly, Zeng and Sycara [Zeng and Sycara1997] study learning to predict agent actions in the context of sequential negotiation. In contrast, we focus on learning how agent actions affect each other. While some of this knowledge could be used to predict the reasoning of other agents, it does not directly predict their actions.
Some of the work closest to our own focuses on learning the effects of environmental context on the outcomes of agent actions. For example, Schmill, Rosenstein, Cohen, and Utgoff [Schmill et al.1998] use decision trees to learn the environmental states and actions that produce changes in particular sensor values of a mobile robot. Similarly, Haigh and Veloso [Haigh and Veloso1998] learn situation-dependent costs of actions from execution traces of robot navigation. This work and other similar work focuses on the relationships among actions and outcomes, a notion closely allied with our focus on actions and their non-local effects (NLEs) in a multiagent context. However, the ``environment'' in our work consists almost entirely of the actions of other agents, and the desired knowledge concerns how to coordinate the actions of multiple agents.
We investigated learning techniques for TÆMS, an existing framework for multiagent coordination. TÆMS [Decker and Lesser1993] represents quantitative information about agent activities, including candidate actions and how those actions can combine to achieve high-level tasks. TÆMS represents a task as a tree whose root is the overall task and whose leaves are primitive actions referred to as methods. Internal nodes represent subtasks composed of other tasks and methods. Internal nodes also specify how the constituent methods and tasks combine for successful execution (e.g., all must execute successfully, or only a single alternative must execute successfully). In addition to this structural information about tasks and methods, TÆMS represents two types of statistical information -- 1) probability distributions that describe the possible values of performance parameters of a method (e.g., the quality of a method's result, the cost of the method, and its duration); and 2) non-local effects (NLEs) of one method on another (e.g., enables, disables, facilitates, and hinders).
Reasoners can use the knowledge represented in TÆMS [Wagner et al.1998a] to evaluate the quality, cost, and duration of possible courses of action and their effects on other agent's actions. Using this information, reasoners can select the one that best1 meets the current constraints and environmental conditions. For example, in a time-constrained situation, an agent may sacrifice solution quality, and pay a larger fee, to produce a result within the specified deadline. Detailed discussions of TÆMS are provided elsewhere [Decker and Lesser1993,Wagner et al.1998b].
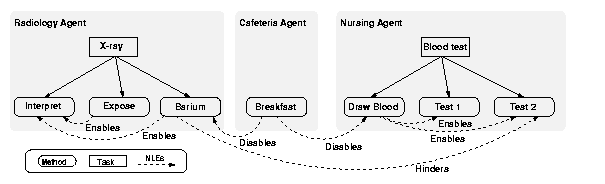
For example, consider how TÆMS could be used to coordinate the tasks assigned to different departments in a hospital. The departments need to coordinate the execution of these tasks to produce maximum medical benefit to patients under time and cost constraints. For a given patient, the radiology department may wish to schedule an x-ray, the nursing staff may wish to draw blood for diagnostic tests, and the cafeteria may wish to provide breakfast for the patient. The existence of NLEs among the methods needed to complete these tasks implies a specific order of execution. For example, eating breakfast may disable some diagnostic tests and the radioactive elements ingested for some x-rays may hinder obtaining accurate results from blood tests. These constraints imply a schedule with the order: blood tests, x-rays, and breakfast.
To be more specific, Figure 1 shows a partial TÆMS task structure for the hospital agents [Decker and Li1998] coordinating their services for a single patient. Radiology has the task of taking an x-ray of the patient. This task requires execution of three methods: providing a barium solution for the patient to ingest, producing an exposure of the patient, and interpreting the exposure. The barium solution enables the interpretation (without it the interpretation would always have zero quality) and the exposure enables the interpretation. Similarly, the nursing staff wish to conduct tests on the patient's blood. The first method of this activity, drawing blood, enables the two tests. One of the tests is hindered if the patient has ingested a barium solution. Finally, hospital policy requires that blood be drawn and barium solutions be administered when the patient has an empty stomach.
This paper focuses on learning the statistical knowledge encoded in TÆMS about distributions and NLEs (distributions were left off figure 1 for simplicity). In particular, we focus on learning four of the most common NLEs - enables, disables, facilitates, and hinders. Each NLE defines a relation between one task or method (A) and another task or method (B). For clarity and brevity, only effects on quality are discussed; effects on duration and cost can be inferred from context. Similarly, the term ``precede'' is used to mean that a method successfully completes execution prior the the beginning of execution for another method.
To learn distributions and NLEs, agents monitor the performance of schedules -- finite sets of methods with at least a partial order. Each learning instance consists of the performance characteristics of a given method in the schedule (e.g., quality, duration, and cost) and the set of all methods in the schedule that successfully c
Our work focuses on learning accurate knowledge of distributions and NLEs. We assume that agents already know what methods are available to be executed, and how to use TÆMS knowledge to produce effective schedules.
To learn distributions and NLEs, agents monitor the performance of schedules -- finite sets of methods with at least a partial order. Each learning instance consists of the performance characteristics of a given method in the schedule (e.g., quality, duration, and cost) and the set of all methods in the schedule that successfully completed execution prior to the given method.2 We assume that all methods in a schedule are either executed directly by the learning agent, or that the learning agent is informed of their execution. Agents are not required to infer the existence of hidden methods. Further, we assume that each schedule execution is independent; methods executed in one schedule do not affect methods executed in another schedule. This limits the scope of NLEs to methods in the schedule, consistent with the original assumptions of TÆMS.
The goal is to use learning instances to infer distributions of
unaffected performance characteristics (quality, duration, and cost)
for each method and to infer the existence of all NLEs and their
associated power factors (![]() ). To acquire this knowledge, we
built the TÆMS Learning System ( TLS). TLS uses three relatively
simple learning methods: 1) empirical frequency distributions; 2)
deterministic properties of schedules; and 3) linear regression.
Below, we discuss each method individually and discuss the
interactions among the methods that allow them to be effective.
). To acquire this knowledge, we
built the TÆMS Learning System ( TLS). TLS uses three relatively
simple learning methods: 1) empirical frequency distributions; 2)
deterministic properties of schedules; and 3) linear regression.
Below, we discuss each method individually and discuss the
interactions among the methods that allow them to be effective.
Empirical frequency distributions are used to estimate
distributions of performance parameters such as quality,
duration, and cost. The frequency distribution for a given
method and performance parameter is derived from a moving window
of k instances of the execution of that method. Our goal is to
estimate the distribution when unaffected by NLEs (i.e.,
the quality of method C may be affected by methods
A and B that facilitate its execution). As a result,
nearly all values are assumed to be affected by NLEs, and they
are divided by the current estimates of the relevant power
factors to render an estimate of the unaffected quality.
For example, if A and B were the only methods currently
thought to affect C, then
![]() .
.
An alternative approach is to learn from only those results of method executions that are guaranteed to be unaffected (e.g., the results of methods executed at the start of each schedule). In empirical tests, this approach proved far slower than the methods reported here. Figure 2 shows the results of one experiment. The top line shows the error associated with learning from only quality values guaranteed to be unaffected. The bottom line shows the error associated with learning from all values, when whose values are corrected based on estimated power factors.
Deterministic properties of schedules are used to learn ``hard'' NLEs such as enables and disables. Although we derived a total of six such properties, two proved particularly useful in the experiments reported here. The first, enables exclusion states that successful execution of method A at any point in a schedule excludes all methods that did not precede A as possible enabling conditions (TÆMS requires that all enabling methods precede a given method for it to execute successfully). The second, disables exclusion states that successful execution of method A at any point in a schedule excludes all methods that precede A as possible disabling conditions (TÆMS specifies that any disabling method preceding a given method will disable it).
Linear regression is used to infer the existence of ``soft'' NLEs
and to estimate their associated power factors (![]() ). Recall
the TÆMS specification of how facilitates and hinders
affect the performance characteristics of methods. For example,
the quality of a given method m0 is determined by its
unaffected quality (
). Recall
the TÆMS specification of how facilitates and hinders
affect the performance characteristics of methods. For example,
the quality of a given method m0 is determined by its
unaffected quality (
![]() )
and the power
factors of methods that facilitate or hinder it (e.g., m1,
m2, and m3). Given these NLEs, TÆMS specifies that:
)
and the power
factors of methods that facilitate or hinder it (e.g., m1,
m2, and m3). Given these NLEs, TÆMS specifies that:
where xn=1 when mn precedes m0 and xn=0 otherwise. Taking the log of both sides:
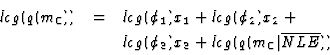
This equation is in the classic form of a linear regression
equation:
![]() ,
where y corresponds to the log of the affected
quality and
,
where y corresponds to the log of the affected
quality and ![]() ,
,
![]() ,
and
,
and ![]() correspond to the logs of the respective power factors.
correspond to the logs of the respective power factors.
![]() and
and ![]() combine to correspond to the
unaffected quality distribution, where
combine to correspond to the
unaffected quality distribution, where ![]() is the
distribution's mean and
is the
distribution's mean and ![]() corresponds to the random
deviations of its values from that mean.
corresponds to the random
deviations of its values from that mean.
To find NLEs affecting each method, we search for equations
containing power factors ![]() that are significantly different than
one (represented by regression coefficients
that are significantly different than
one (represented by regression coefficients ![]() significantly
different from zero). We conduct this search using a standard
statistical method, stepwise linear regression [Draper and Smith1981,Neter et al.1990]. Stepwise
regression conducts a simple local search over possible regression
equations, starting with an equation containing only
significantly
different from zero). We conduct this search using a standard
statistical method, stepwise linear regression [Draper and Smith1981,Neter et al.1990]. Stepwise
regression conducts a simple local search over possible regression
equations, starting with an equation containing only ![]() and
ending with an equation containing at most k terms, where k is the
number of methods available in each schedule. Terms are added to the
equation if their coefficients are significantly different than one,
and are removed if their coefficients are not significantly different
than one (coefficients of existing terms in an equation can
change when new terms are added).
and
ending with an equation containing at most k terms, where k is the
number of methods available in each schedule. Terms are added to the
equation if their coefficients are significantly different than one,
and are removed if their coefficients are not significantly different
than one (coefficients of existing terms in an equation can
change when new terms are added).
Three assumptions of linear regression create potential problems for applying the technique to learn power factors for soft NLEs. Under the first assumption, independence of the variables xn, knowing a value of one x should tell us nothing about the value of any other x. Unfortunately, hard NLEs can cause successful execution of some methods to be dependent on the successful execution of others, introducing dependence among the variables xn. The NLE A enables B introduces a positive correlation between xA and xB; A disables B introduces a negative correlation. Regression is robust against moderate violations of this assumption, but strong violations can greatly increase the variance of estimated coefficients of the regression equation (in our case, causing the estimates of power factors to be extremely inflated or deflated). TLS addresses this problem in two ways. First, it checks for strong violations of this assumption (often referred to as perfect multicollinearity), and doesn't alter the current state of knowledge in such cases. In our experiments, such violations typically occurred only in very small datasets. Second, TLS uses stepwise regression which greatly reduces the total number of variables in regression equations, thus reducing the probability that two or more of them will be dependent.
Under the second assumption, normally-distributed errors, the
distribution of the error term in the regression equation should
be normal. In our case, the error term represents the log of the
unaffected quality distribution
![]() (shifted so its mean is zero). To match this assumption, the
distribution itself should be log-normal. While this is one
reasonable quality distribution, it is not the only reasonable
one. We experiment with an alternative distribution to indicate
how linear regression is robust to moderate violations of this
assumption.
(shifted so its mean is zero). To match this assumption, the
distribution itself should be log-normal. While this is one
reasonable quality distribution, it is not the only reasonable
one. We experiment with an alternative distribution to indicate
how linear regression is robust to moderate violations of this
assumption.
The third assumption affects how we test statistical
significance. Such tests are run to determine which coefficients
![]() differ significantly from zero. The stringency of any
one test is determined by
differ significantly from zero. The stringency of any
one test is determined by
![]() ,
which indicates the
probability of a Type I error (incorrectly rejecting the null
hypothesis that a single coefficient is zero). However, for a
single performance parameter (e.g., quality) and k methods in a
schedule, k(k-1) possible NLEs exist. TLS tests whether each
of these NLEs exists. Under these conditions, the probability of
TLS making at least one Type I error is much larger than
,
which indicates the
probability of a Type I error (incorrectly rejecting the null
hypothesis that a single coefficient is zero). However, for a
single performance parameter (e.g., quality) and k methods in a
schedule, k(k-1) possible NLEs exist. TLS tests whether each
of these NLEs exists. Under these conditions, the probability of
TLS making at least one Type I error is much larger than
![]() .
If the NLEs are independent, the probability is:
.
If the NLEs are independent, the probability is:
For example, for the overall probability of error
![]() to be small (e.g., 0.10) in our base case experiment, the
probability of error on any one test
to be small (e.g., 0.10) in our base case experiment, the
probability of error on any one test
![]() must be much
smaller (0.000012). This process is called Bonferroni
adjustment. Some such adjustment is important in any context
where many explicit or implicit hypothesis tests are made
[Jensen and Cohen1999]. TLS uses Bonferroni adjustment to set
appropriate values of
must be much
smaller (0.000012). This process is called Bonferroni
adjustment. Some such adjustment is important in any context
where many explicit or implicit hypothesis tests are made
[Jensen and Cohen1999]. TLS uses Bonferroni adjustment to set
appropriate values of
![]() so that
so that
![]() is
small.
is
small.
In each experiment, agents create learning data by generating and executing schedules. In all experiments reported here, agents operate in an exploration mode, executing randomly-generated schedules, rather than attempting to use already learned knowledge to generate maximally effective schedules. In practice, agents are likely to mix exploration and exploitation of learned knowledge, and even to use directed exploration. These options will be explored in later work.
Agents have access to performance parameters of executed schedules -- values of quality, duration, and cost for each method in a schedule -- that are affected by an initially unknown set of NLEs. The actual unaffected distributions and NLEs are hidden from agents, but they determine the values of performance parameters observed by agents.
Consistent with other projects using TÆMS, we use discrete probability distributions. However, our methods for learning hard and soft NLEs apply equally well to cases with continuous probability distributions, and a
We measure the effectiveness of TLS with metrics that directly measure the quality of the learned knowledge, rather than indirectly measuring its effect on agent coordination. This approach focuses evaluation on TLS and avoids confounding TLS' performance with the performance of other system components for scheduling and coordination [Wagner et al.1997]. However, it could also inappropriately credit or penalize TLS for learning knowledge that is unimportant or infrequently used, respectively. To guard against this latter error, we review the utility of the learned knowledge at the the next section and show that the most useful knowledge is generally learned most quickly.
In each experiment, agents create learning data by generating and executing schedules. In all experiments reported here, agents operate in an exploration mode, executing randomly-generated schedules, rather than attempting to use already learned knowledge to generate maximally effective schedules. In practice, agents are likely to mix exploration and exploitation of learned knowledge, and even to use directed exploration. These options will be explored in later work.
Agents have access to performance parameters of executed schedules -- values of quality, duration, and cost for each method in a schedule -- that are affected by an initially unknown set of NLEs. The actual unaffected distributions and NLEs are hidden from agents, but they determine the values of performance parameters observed by agents.
Consistent with other projects using TÆMS, we use discrete probability distributions. However, our methods for learning hard and soft NLEs apply equally well to cases with continuous probability distributions, and a method such as kernel density estimators [John and Langley1995] could be used to estimate continuous probability distributions from empirical data.
The experiments were conducted in two phases. First, a base case was
run with settings corresponding to the assumptions of the learning
techniques, particularly linear regression. Second, those settings
were systematically altered to test the effects of violations of those
assumptions. For the base case, schedules contain 30 unique methods,
executed in a random order. Method performance is controlled by a
TÆMS task structure containing 15 NLEs (three disables, four
enables, four facilitates, and four hinders). In addition, the task
structure avoids cases where a single method is affected by more than
one NLE. Values of ![]() for the soft NLEs deviate moderately from
unity (3.0 for facilitate and 0.5 for hinders). The discrete
probability distributions for performance parameters of methods (e.g.,
quality) are approximately log-normal. To learn empirical frequency
distributions, TLS uses a window size of 100, and to learn soft
NLEs, it uses
for the soft NLEs deviate moderately from
unity (3.0 for facilitate and 0.5 for hinders). The discrete
probability distributions for performance parameters of methods (e.g.,
quality) are approximately log-normal. To learn empirical frequency
distributions, TLS uses a window size of 100, and to learn soft
NLEs, it uses
![]() .
In the next section, we show
results for this base case, and results for dependent NLEs,
log-uniform quality distributions, soft NLEs with small deviations
from unity, and a larger number of soft NLEs.
.
In the next section, we show
results for this base case, and results for dependent NLEs,
log-uniform quality distributions, soft NLEs with small deviations
from unity, and a larger number of soft NLEs.
To measure learning in TLS, we use four error metrics, each of
which applies to one of the three pairs of learning methods and
learned knowledge. TLS' error in learning distributions with
empirical frequencies is measured by the mean difference in areas
(
![]() )
between the cumulative probability plots of the
actual and learned distributions. For example, figure
3 shows how D is calculated for
a method in a particularly simple case. D is normalized by
dividing by the total range of the quality (
qmax-qmin)
so that it varies between 0 and 1. The mean of D,
)
between the cumulative probability plots of the
actual and learned distributions. For example, figure
3 shows how D is calculated for
a method in a particularly simple case. D is normalized by
dividing by the total range of the quality (
qmax-qmin)
so that it varies between 0 and 1. The mean of D,
![]() ,
measures the average D across all methods.
,
measures the average D across all methods.
TLS' error in learning hard NLEs with deterministic properties is measured by the proportion of misclassified hard NLEs (H). All experiments reported in this paper begin with the assumption that all possible hard NLEs exist -- a total of k(k-1) possible hard NLEs among k methods. Deterministic properties are then used to eliminate hard NLEs until only true ones remain. The deterministic properties used by TLS are guaranteed to preserve actual hard NLEs, thus H always measures the extra NLEs that the system was unable to eliminate from consideration.
TLS' error in learning soft NLEs with stepwise linear regression
is measured by two different metrics. The first measures the
errors in TLS' inferences about which soft NLEs exist;
the second measures the errors in TLS' estimates of the
power factors for inferred NLEs. The first metric, S,
is the proportion of all true soft NLEs that are learned
correctly (number of soft NLEs learned / number
of true soft NLEs). In the base case used in the experiments,
there are eight soft NLEs. The second metric,
![]() ,
is the average difference between the actual
power factor and the learned power factor. For a given soft NLE
i,
,
is the average difference between the actual
power factor and the learned power factor. For a given soft NLE
i,
![]() ). The
mean difference,
). The
mean difference,
![]() ,
measures the average
,
measures the average
![]() across all possible soft NLEs.
across all possible soft NLEs.
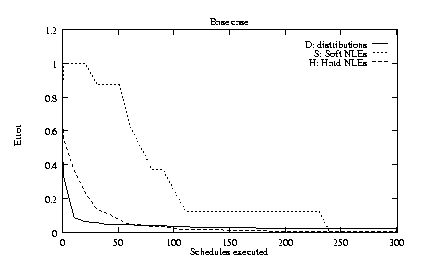
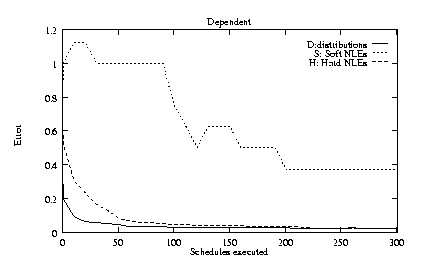
Figure 5a shows the values of the first three error
metrics (excluding
![]() )
for the base conditions (the
settings outlined above). In fewer than 100 schedules, the
distributions and hard NLEs are learned with low error. TLS
continues to reduce the number of spurious hard NLEs, reaching
one by the time 300 schedules are executed. The existence of all
soft NLEs is not correctly inferred until more than 240 schedules
have been executed, although all but one is inferred in less than 150
schedules.
)
for the base conditions (the
settings outlined above). In fewer than 100 schedules, the
distributions and hard NLEs are learned with low error. TLS
continues to reduce the number of spurious hard NLEs, reaching
one by the time 300 schedules are executed. The existence of all
soft NLEs is not correctly inferred until more than 240 schedules
have been executed, although all but one is inferred in less than 150
schedules.
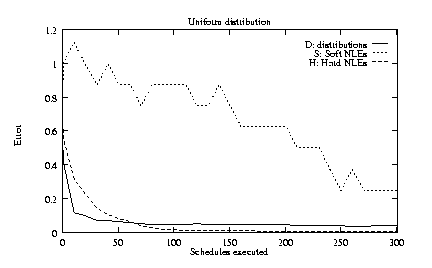
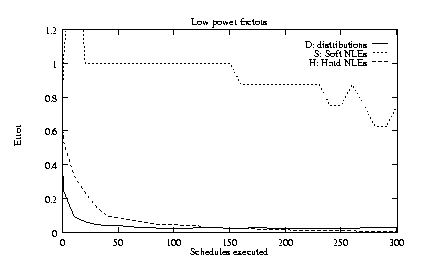
To explore the robustness of TLS, we tested four alternatives
to the base conditions:
1) dependent NLEs rather than independent NLEs;
2) log-uniform quality distributions rather than log-normal;
3)
![]() and
and
![]() rather
than
rather
than
![]() and
and
![]() ;
and
4) 15 soft NLEs rather than 8 soft and 7 hard.
;
and
4) 15 soft NLEs rather than 8 soft and 7 hard.
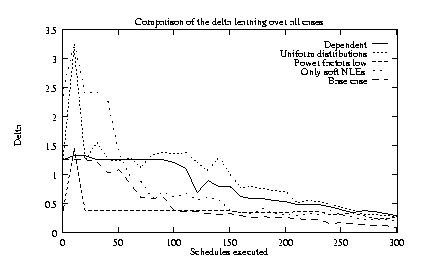
Figure 5b shows the sum of the errors in the power
factors, ![]() ,
for the base conditions and all four
alternative conditions. All tend toward zero as the number of
schedule executions increases, but the base conditions cause the
fastest convergence. Decreasing the deviations of the power
factors from one causes a long plateau before sufficient data
accumulate to begin learning these small deviations. Similarly,
dependence among the NLEs also causes a plateau, because the hard
NLEs prevent some methods from executing, depriving the
regression of the data needed to infer soft NLEs. A log-uniform
distribution causes larger errors in power factors.
,
for the base conditions and all four
alternative conditions. All tend toward zero as the number of
schedule executions increases, but the base conditions cause the
fastest convergence. Decreasing the deviations of the power
factors from one causes a long plateau before sufficient data
accumulate to begin learning these small deviations. Similarly,
dependence among the NLEs also causes a plateau, because the hard
NLEs prevent some methods from executing, depriving the
regression of the data needed to infer soft NLEs. A log-uniform
distribution causes larger errors in power factors.
One result that figures 5a and b do not convey clearly is the degree to which distributions are learned correctly. Figure 4 shows a cumulative probability plot comparing an actual distribution and a learned distribution for a method affected by a single hinders under the base conditions. The plot shows the distribution after 300 schedules. The learned distribution closely approximates the actual distribution.
 |
 |
 |
 |
 |
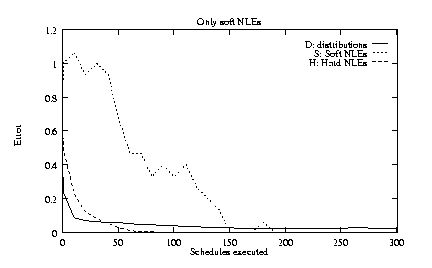 |
Figure 5a shows the values of the first three error
metrics (excluding
![]() ) for the base conditions (the
settings outlined above). In fewer than 100 schedules, the
distributions and hard NLEs are learned with low error. TLS
continues to reduce the number of spurious hard NLEs, reaching
one by the time 300 schedules are executed. The existence of all
soft NLEs is not correctly inferred until more than 240 schedules
have been executed, although all but one is inferred in less than 150
schedules.
) for the base conditions (the
settings outlined above). In fewer than 100 schedules, the
distributions and hard NLEs are learned with low error. TLS
continues to reduce the number of spurious hard NLEs, reaching
one by the time 300 schedules are executed. The existence of all
soft NLEs is not correctly inferred until more than 240 schedules
have been executed, although all but one is inferred in less than 150
schedules.
To explore the robustness of TLS, we tested four alternatives
to the base conditions:
1) dependent NLEs rather than independent NLEs;
2) log-uniform quality distributions rather than log-normal;
3)
![]() and
and
![]() rather
than
rather
than
![]() and
and
![]() ; and
4) 15 soft NLEs rather than 8 soft and 7 hard.
; and
4) 15 soft NLEs rather than 8 soft and 7 hard.
Figure 5b shows the sum of the errors in the power
factors, ![]() , for the base conditions and all four
alternative conditions. All tend toward zero as the number of
schedule executions increases, but the base conditions cause the
fastest convergence. Decreasing the deviations of the power
factors from one causes a long plateau before sufficient data
accumulate to begin learning these small deviations. Similarly,
dependence among the NLEs also causes a plateau, because the hard
NLEs prevent some methods from executing, depriving the
regression of the data needed to infer soft NLEs. A log-uniform
distribution causes larger errors in power factors.
, for the base conditions and all four
alternative conditions. All tend toward zero as the number of
schedule executions increases, but the base conditions cause the
fastest convergence. Decreasing the deviations of the power
factors from one causes a long plateau before sufficient data
accumulate to begin learning these small deviations. Similarly,
dependence among the NLEs also causes a plateau, because the hard
NLEs prevent some methods from executing, depriving the
regression of the data needed to infer soft NLEs. A log-uniform
distribution causes larger errors in power factors.
One result that figures 5a and b do not convey clearly is the degree to which distributions are learned correctly. Figure 4 shows a cumulative probability plot comparing an actual distribution and a learned distribution for a method affected by a single hinders under the base conditions. The plot shows the distribution after 300 schedules. The learned distribution closely approximates the actual distribution.
Figures 5c-f show the same content as figure 5a, but for the four alternative conditions outlined above. In these alternative conditions, distributions and hard NLEs are still learned very rapidly, but the speed with which soft NLEs can be inferred is generally reduced.
The experiments revealed some unexpected difficulties in learning. For example, the overall low error rate for NLEs masks some subtle limitations that prevents TLS from accurately learning all NLEs when such relationships are dependent (e.g., Figure 5c). The situation shown in figure 6 demonstrates three cases of such limitations. The disables between M1 and M3 is spurious, but cannot be eliminated. For any schedule in which M1 precedes M3, M3 will be disabled because of the valid hard NLEs connecting M1, M2, and M3, thus simulating a disables between M1 and M3. For the same reason, the hinders between M1 and M3 cannot be learned. Finally, the spurious disables between M1 and M2 cannot be eliminated because the valid enables NLE between the two methods prevents M1 from every preceding M2. Fortunately, much of the knowledge made inaccessible by these limitations concerns ``impossible schedules'' -- schedules that could never be executed in practice. However, future versions of TLS will account for this minor pathology.
The error graphs in figure 5 also indicate how the most important coordination knowledge is often learned most quickly. For example, TLS learns large power factors more quickly than small factors, and it learns hard NLEs (e.g., enables and disables) much more quickly than soft NLEs. Though not shown in experiments, empirical probability distributions learn the probabilities of the most frequent values of distributions most rapidly.
These learned NLEs may act among the local methods of one agent, or methods in several different agents (as indicated in the hospital scheduling example). Although we experiment with a single agent learning quantitative coordination knowledge, TLS is fully able to learn NLEs across multiple agents if each agent has access to the schedule and execution characteristics of methods. We have already designed a distributed version of TLS, where each agent exchanges executed schedules for learning. In this design, we can have several agents using TLS to learn only those NLEs that affect their own methods or one dedicated learning agent that learns for the whole community.
Effort partially sponsored by the Defense Advanced Research Projects Agency (DARPA) and Air Force Research Laboratory Air Force Materiel Command, USAF, under agreement number F30602-97-1-0249. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon.This material is based upon work supported by the National Science Foundation under Grant No.IIS-9812755. Disclaimer: The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the Defense Advanced Research Projects Agency (DARPA), Air Force Research Laboratory, National Science Foundation, or the U.S. Government.
Effort partially sponsored by the Defense Advanced Research Projects Agency (DARPA) and Air Force Research Laboratory Air Force Materiel Command, USAF, under agreement number F30602-97-1-0249. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon.This material is based upon work supported by the National Science Foundation under Grant No.IIS-9812755. Disclaimer: The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the Defense Advanced Research Projects Agency (DARPA), Air Force Research Laboratory, National Science Foundation, or the U.S. Government.
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -font_size 11pt -html_version 3.2 -white -address vincent@cs.umass.edu -no_navigation -dir html tr-article.tex.
The translation was initiated by Regis Vincent on 1999-04-06
This paper has been published by the American Association for Artificial Intelligence (http://www.aaai.org)
This document has been copyrighted by the American Association for Artificial Intelligence and is being made available solely for the use and benefit of authors preparing papers for AAAI Press publications. No other use of this document may be made without permission in writing from the copyright holder.